论文阅读-Randomized Bit Vector：Privacy-Preserving Encoding Mechanism

文章地址：https://dl.acm.org/citation.cfm?id=3271703&dl=ACM&coll=DL
标题：Randomized Bit Vector：Privacy-Preserving Encoding Mechanism
作者：Lin Sun; Lan Zhang; Xiaojun Ye
发表会议：Proceedings of the 27th ACM International Conference on Information and Knowledge Management

---

本文发表于CIKM18，是上篇BV工作内容的扩展，由BV机制扩展到RBV机制，同时将RBV进行了两个方面的扩充：1、将差分隐私性质加入到RBV中形成了DPRL编码方案；2、将河豚机制（Pufferfish Mechanism）机制的性质假如到RBV中形成PMRL方案。实验表明这些方法都可以在PPRL问题中取得不错的实验效果。

下面是本文的笔记，序号和论文中的序号一样，有些地方我觉得对这篇文章的理解不重要，我跳过了，建议先看一下原文再来看我的笔记。

• 1 Introduction
• 2 Related Work
• 3 Embedding Numerical Values with Randomized Hashing Functions
  • 3.1 The fundamental RBV algorithm
  • 3.2 Optimal number of random variables
  • 3.3 Differential Privacy with Record Linkage
• 4 Pufferfish Mechanism with Laplace Noise
• 5 Experiments
• 6 总结与反思

1 Introduction

在之前的文章《Distance-Aware Encoding of Numerical Values for Privacy-Preserving Record Linkage》中，我们介绍了什么是基本的 PPRL 问题，也介绍了当前 PPRL for Numerical Values 面对的挑战，因此背景部分这里就不再提及，可以参考那篇文章。

2 Related Work

这部分作者介绍了文章中用到的隐私保护理论基础和当前的相关工作，在当前的技术中提到了布隆过滤器（bloom filter）。在很多方面，布隆过滤器都发挥着很大的作用，下次将会更新基于布隆过滤器的数字Record Linkage方案，本文就先不详细介绍了。背景中的Bit Vectors方案在上一篇文章中已经提及，就不再细说了，虽然在介绍的时候是发在ICDE上的短文，可是这个工作现在已经经过扩充，发表在期刊TKDE中，其论文名为：FEDERAL: A Framework for Distance-Aware Privacy-Preserving Record Linkage。在理论上，这方面的工作和之前的短文相比，并没有很多扩充。

同时，这里需要知道一个叫Pufferfish Mechanism的东西。之前我们在提到隐私保护的时候，都是提到的差分隐私。本文中提到了一个叫做河豚机制的东西（Pufferfish Mechanism，当然，我也不知道为什么取这个名字）。河豚机制中有几个要素：

• 秘密集$S$
• 秘密对$Q$
• 可能的数据分布

其中，秘密对$Q$是$S\times S$的子集，即$Q \subseteq S \times S$。河豚机制的定义和差分隐私差不多，可以用这个方程表示：

$$e^{-\epsilon} \le \frac{\Pr_{\mathcal{M,\theta}}[\mathcal{M}(X)=w|s_i,\theta]}{\Pr_{\mathcal{M,\theta}}[\mathcal{M}(X)=w|s_j,\theta]} \le e^\epsilon$$

即在已知 $s_i$ 的情况下观测的结果和在已知 $s_j$ 的情况下观测得到的结果是类似的，这里的 $(s_i,s_j)$ 就是 $Q$ 的元素。

即河豚机制的出发点和 DP 不同，我们不需要保证任意的两个元素都具备不可区分的特性（这是差分隐私的保证），我们只需要保证给定的两个元素不可区分就好了，所以河豚机制中的 $Q$ 是 $S\times S$ 的子集。也正因如此，当 $Q=S\times S$ 的时候，河豚机制其实就等价于差分隐私机制了。

3 Embedding Numerical Values with Randomized Hashing Functions

接触RBV之前，还是需要提及一下之前的BV方案。在BV方案中，首先定义了基于随机数的哈希函数：

$$h_i(x) = \begin{cases} 1 & x \in [r_i - t, r_i + t] \\ 0 & \text{Otherwise} \\ \end{cases}$$

也就是说，根据当前随机数生成一个定长的区间。那么如果两个数相近的话，那么这两个数很可能就在同样的一个区间里面了。所以，BV的编码过程是这样的：

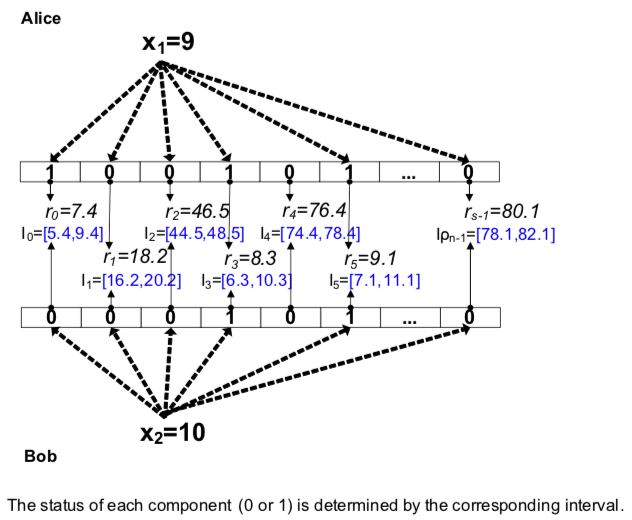
由于BV的编码机制，其缺点也非常明显，即只能比较的差最多为 $2t$，因为当距离大于 $2t$ 时，所有的区间都不会有重叠。

3.1 The fundamental RBV algorithm

那么如何解决BV的限制呢，我们可以尝试改变BV中的哈希函数，如下：

$$h_i(x) = \begin{cases} 1 & x \ge r_i \\ 0 & x < r_i \\ \end{cases}$$

也就是说，将原本的定长区间改成现在的不定长区间，在这种情况下，编码的过程就变成这样了（给定s个随机数）：

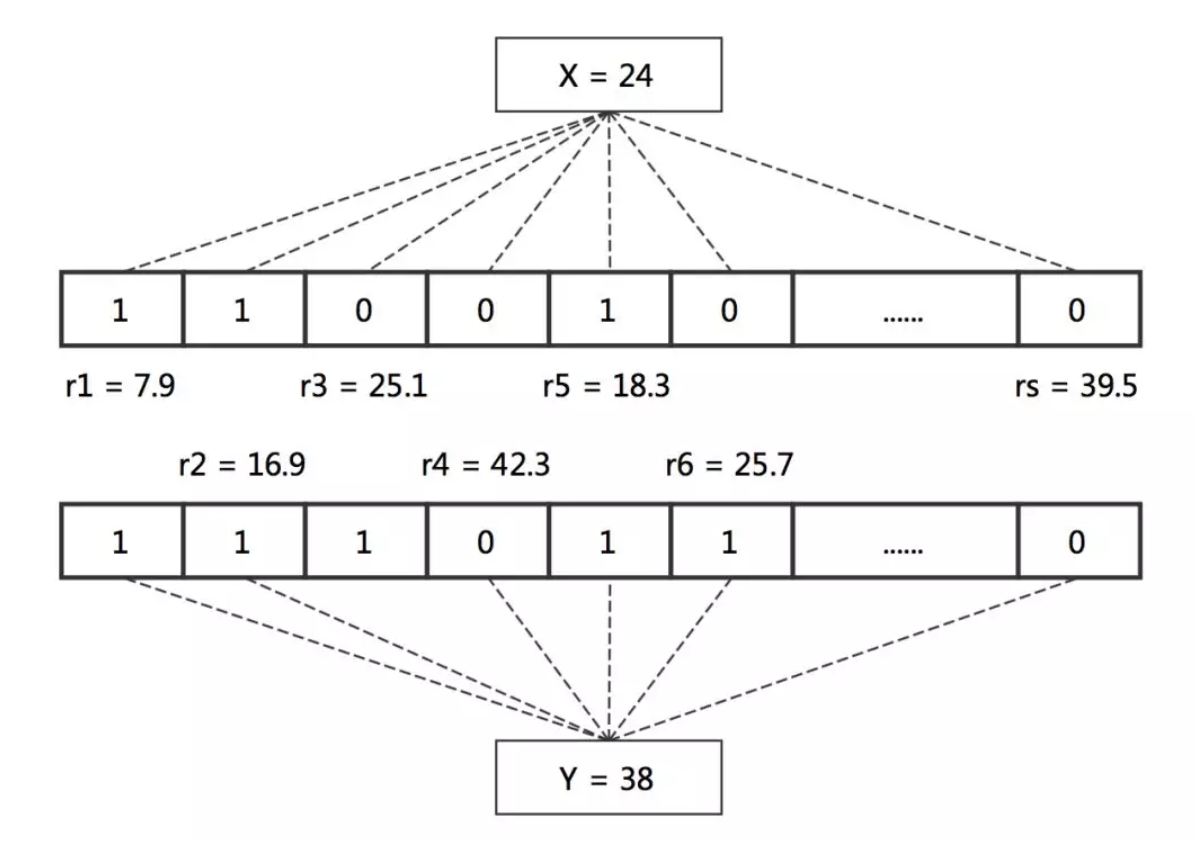
然后论文中给了几个引理：

Lemma 3.1 Excepted elemetns: The expected number $w(x)$ of elements which are set in $rbv$ is:

$$E[w(x)] = s \cdot \frac{x-lower}{u}$$

Lemma 3.2 Expected common elements: The excepted number $v(x_1,x_2)$ of common elements that are set in a pair of binary vectors of $(x_1, x_2)$ with $x_1 < x_2$ is:

$$E[v(x)] = s \cdot \frac{x_1-lower}{u}$$

Theorem 3.3 Expected Hamming distance: Let $d_E = |x_2-x_1|$, then the expected Hamming distance $E[d_H]$ of pair $(x_1, x_2)$ is:

$$E[d_H(x_1, x_2)] = s \cdot \frac{d_E}{u}$$

定理3的证明过程用到了引理3.1和引理3.2。定理3.3 说明欧几里得距离和汉明距离之间有着一种“模糊”的对应关系，比如我们的参数为s=1000，u=100，那么如果欧几里得距离为2的话，期望的汉明距离就是20了，当然每次计算的结果不一样，可能是19，可能是22之类，不过其期望是20。

3.2 Optimal number of random variables

3.1节中说了欧几里得距离和汉明距离之间的模糊对应关系，我们当然希望得到的数据更加接近期望的数据，这样数据估计就会越精确。

只管上来说，如果编码的长度越短，那么对数据差的估计效果就越差，如果编码的长度越长，那么数据差可以更好地还原。那么有没有理论的方法去指导我们如何设置参数呢？作者给出了这样的结论：

Theorem 3.4 Given $\epsilon>0$ and $0<\delta<1$, to ensure $\Pr[d_H\le(1+\epsilon)E[d_H]] \le \delta$, it is sufficient to set:

$$s \ge \lceil \frac{2u \ln \frac{1}{\delta}}{\epsilon \ln(1+\epsilon) d_E} \rceil$$

值得注意的是，定理标题中的一个符号产生了错误，其概率中的第一个小于等于号应该为大于号，否则这个公式就没有意义了。

这个定理是说，只要给定$\epsilon, \delta$表示准确率，那么欧几里得距离几乎可以以任意准确率得以保证，这个公式也说明：$\epsilon, \delta$ 越小，准确率越高，用于编码时的 $s$ 就越大，即编码长度越大。这也符合一开始的理解。

因此，给定任意准确率，我们都可以设置对应的 $s$ 的值，以此来保证编码过程中欧几里得距离估计的准确性。

3.3 Differential Privacy with Record Linkage

对于“安全”这个东西，有着这样一个问题，即，有些东西可能感觉上面是安全的，但是缺乏数学定义。我们只能说那些有理论基础的方案是安全的。

3.1节中提到的RBV方案也是一样的，直观上感觉可能是安全的（因为数据范围和随机数仅仅在双方直接互相协商，不公开）。但是却无法根据现有的隐私保护模型推到而出。当然，这个东西也很奇妙，你也不能说没有隐私保护模型的方案就是不安全的，或许是当前隐私保护模型不够好也不一定，虽然这种可能性较低。

回到RBV方案上来，我们注意到好像当前没有什么模型能说明这个方案是 privacy-preserving 的。所以作者将 Random Response 的机制加到了RBV中。

即数据的编码过程分为两步（和RAPPOR这篇文章中提到的一样）：

1. Encoding：将x编码到randomized bit vector
2. Perturbation：对Encoding的结果中的每一位进行一个替代

现在的过程用图示的话就是这个样子：

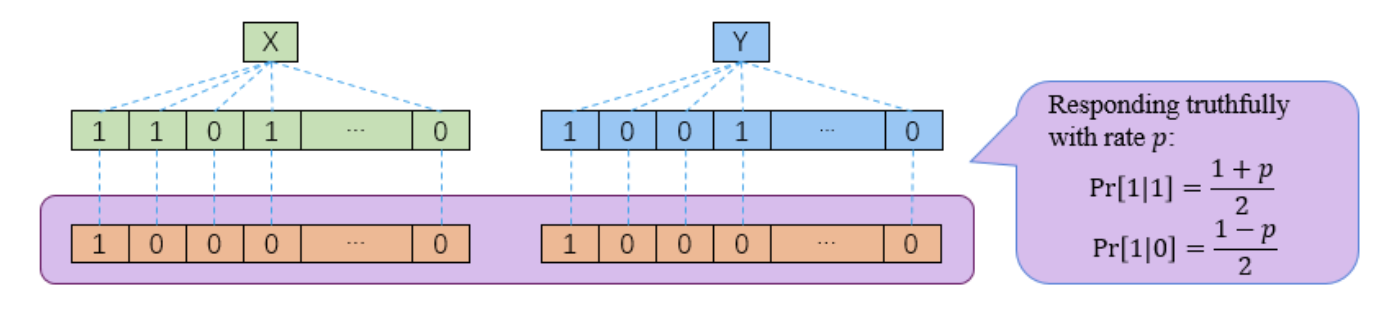
作者说如果只用一位的话，那么这个方案是保持差分隐私的，其隐私保护等级为$ \ln \frac{1+p}{1-p}$。这个证明过程也很容易，就是基于Random Response，没啥技术含量.接下来，作者证明了这个方案在s位的情况下的隐私保护特性：

Theorem 3.6 DP-Composition: The DPRL mechanism with $s$ bits is $(\epsilon, \delta)$-differentially private, when

$$e^\epsilon\cdot(\frac{1-p}{2})^s+\delta=(\frac{1+p}{2})^s$$

证明过程这里就略过了。当然，编码的一切任务都是为了估计出欧几里得距离，所以我们要找到欧几里得距离和汉明距离之间的关系，不能说你提供了安全性就啥也不管了，那样也没有意义。接下来作者给出了两种距离之间的对应关系：

Corollary 3.7 (DP-Hamming Distance): In DPRL, The Ex- pected Hamming Distance $E[d_H]$ of pair $(x1,x2)$ with $d_E = |x1−x2|$ is:

$$E[d_H(x_1,x_2)] =s \cdot (\frac{1-p^2}{2}+\frac{d_E p^2}{u} )$$

证明过程有点长，这里就不贴出来了，只需要基本的数学知识就可以理解了。可以参考原文给出的解释。通过这个公式，我们也可以发现，当p=1时，DPRL机制其实就是RBV机制。

4 Pufferfish Mechanism with Laplace Noise

第三节提出DPRL的出发点是为了提供更强的安全性，而DP提供了全局不可区分性，即任意两个数据在编码结果上来看都是不可区分的。那么我们有必要采用DP吗？

以年龄为例，夸张点来看，如果一个问问你你多大了，你肯定不会说你才三岁，当然你也不想说出具体的年纪大小，特别是如果你是一个女孩子的话。当然，如果在多想一步的话，你也不可能说出你的具体年龄大小，精确到天？还是精确到小时？

所以，“在一定程度上回答”会在一定程度上降低数据有效性，但是会很大程度上提高隐私性。年龄精确到天和精确到年其实数据有效性是差不多的，同样的道理，如果在精确到年的基础上再进行模糊化呢？比如：精确到“十年”？其实数据也是有效的，只不过有效性降低了而已。所以，作者说那我们干脆搞一个数据有效性范围吧，即我们只保证 x 和 [x-△t, x+△t] 中的数据不可区分就好了。所以作者用了 pufferfish mechanism 的机制，即提供局部数据保护。

因此作者又提了一个叫做PMRL的方案，过程很简单：

$$PMRL(x) = RBV(x+\mathcal{N})$$

其中N是要给拉普拉斯噪声，其均值为0，方差为$\sigma$ ，那么怎么设置方差呢？作者给了一个定理。

Theorem 4.1 (PMRL Privacy). To provide $\epsilon$-Pufferfish private in
the PMRL mechanism with single bit, the $\sigma$ in Laplace noise should be:

$$\sigma = \frac{\triangle t}{\epsilon}$$

至于为什么加上这个噪声就可以了，可以参考论文中给出的证明。当然，礼节上来看的话也可以和DP联系到一起，△t可以看成DP中的敏感度，这样的话这个公式就很容易理解了，但是这个结论不能直接这么给出，因为RBV的方案中实际上是自带噪声的，所以需要结合RBV的编码过程一起给出。

5 Experiments

理论部分讲解完了，我们就来看实验了。在看实验之前，可以先看一个不同方案编码的例子：

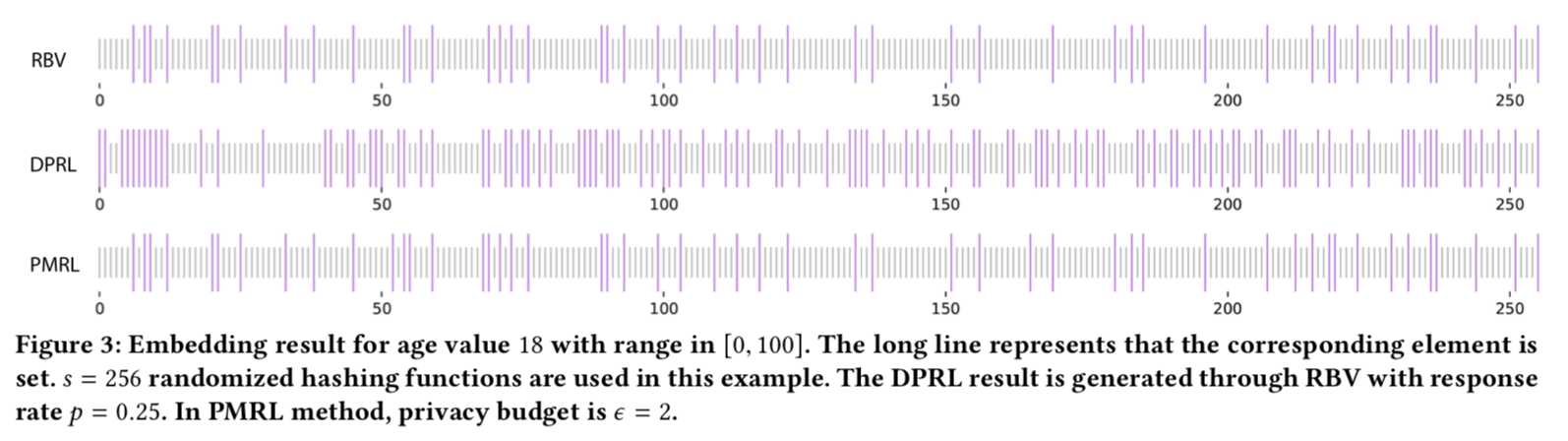
上图是本文中三种方案编码数字18的编码结果。可以看到，不同的方法还是有区别的。

为了让实验过程更具有科学代表性，作者采用了不同的数据分布进行实验，数据集中有公开的数据集和根据一定分布合成的数据集（正态分布和均匀分布）：

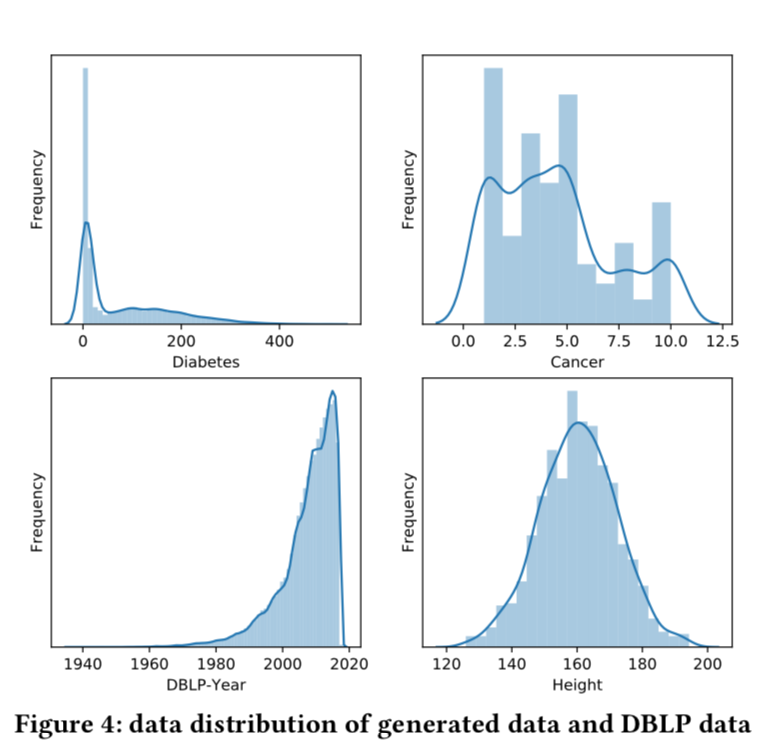
上图是作者画出的不同数据集的数据分布情况，还有一个均匀分布的数据集出于画图美观的需求，就没有列出来了。

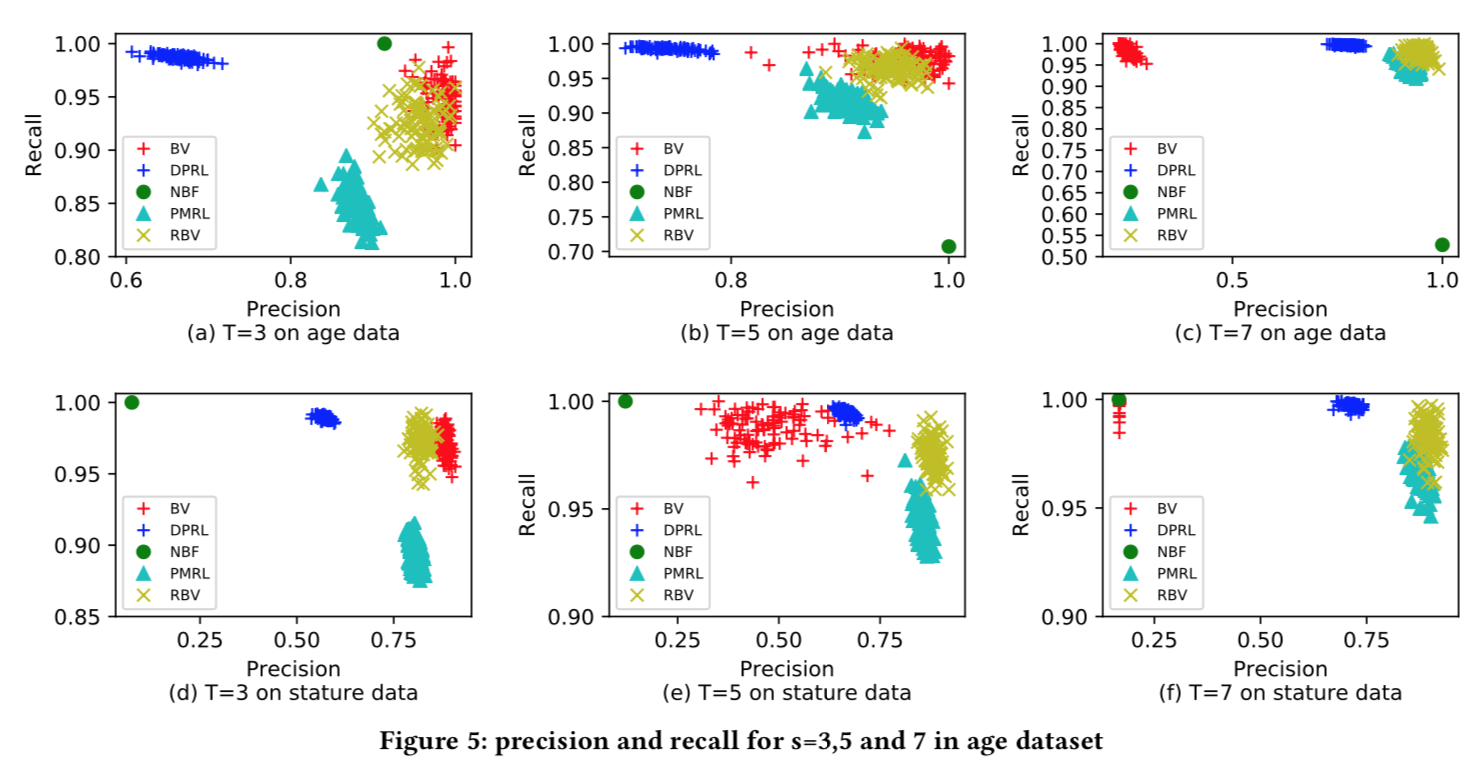
我么可以先来看一下不同方法编码结果的展示，横坐标为precision，纵坐标为recall，可以看到，和当前的其他方案比较来看，效果还是不错的。

另外，再DBLP数据集下也可以看到效果还是很好的，同时我们可以看到DPRL和PMRL方案都有隐私保护理论基础，同时效果还很好。

另外一组实验是来说明BV的缺陷的：

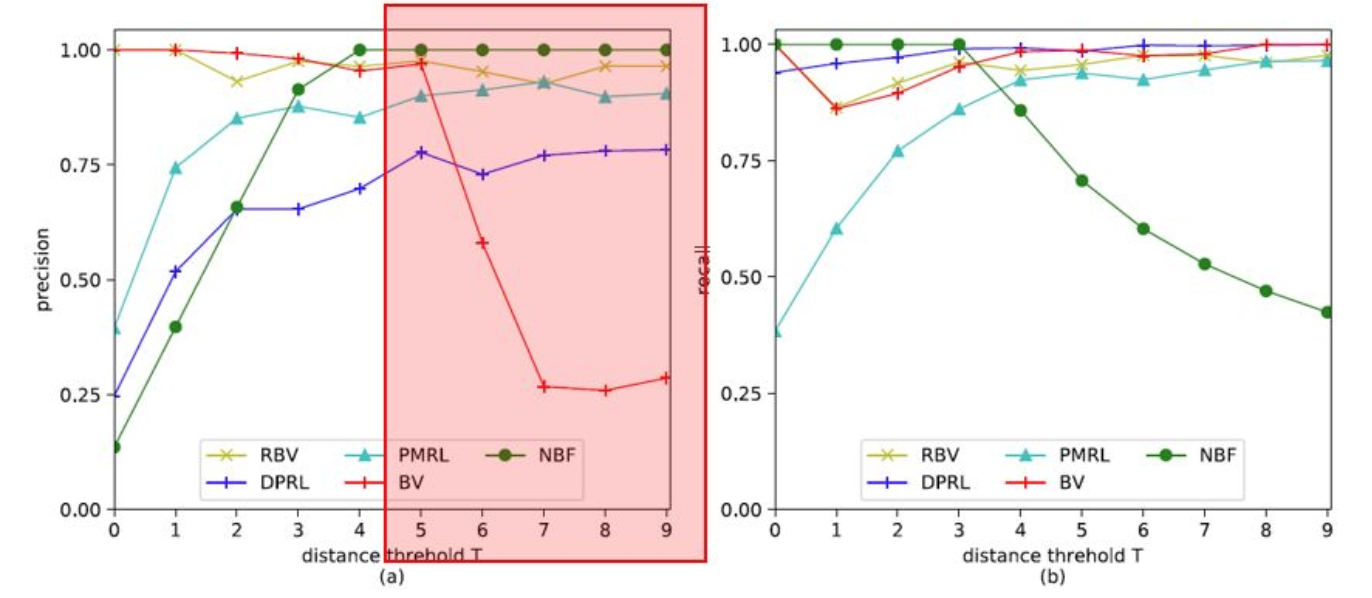
我们之前说过BV机制只能提供2t范围内的欧几里得距离估计，这个实验也说明了这一点。那么这会带来什么缺陷呢？

就是这些方案不支持低相似度数据比较，可以看这个图：

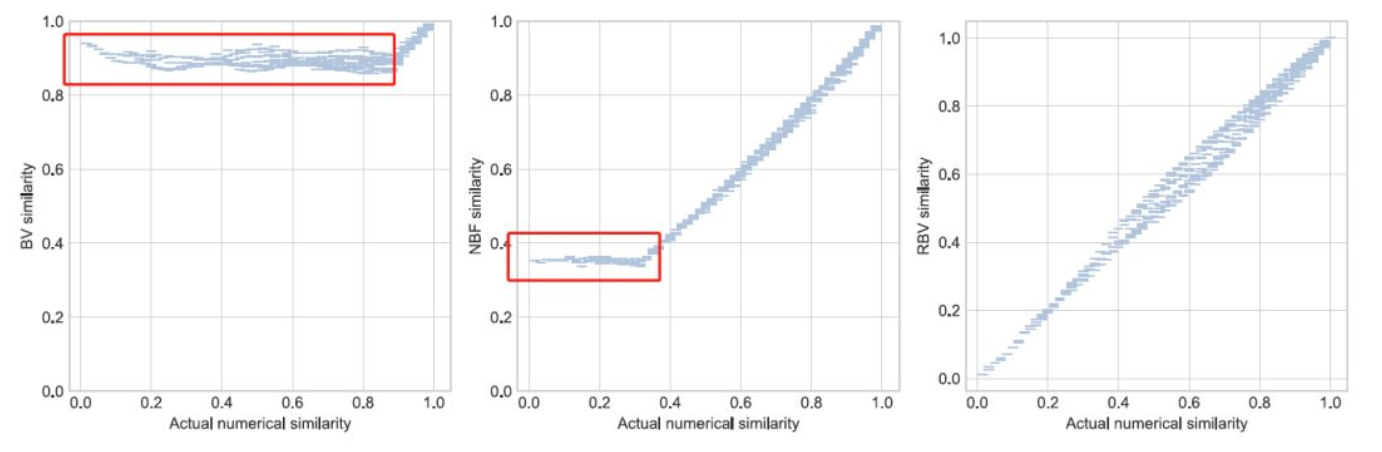
这个图里面我们就发现了BV机制和NBF机制的相似度不是线性的，所以只能用来比较高相似度的数据。

作者进行的最后的实验是探究编码过程的参数对实验效果的影响，首先是编码长度的影响：

可以看到编码的长度越长，实验的效果越好。

同时，作者也通过实验的方式告诉了读者，如果实验追求的是f-score，那么该如何再汉明空间中设置欧几里得距离对应的阈值：

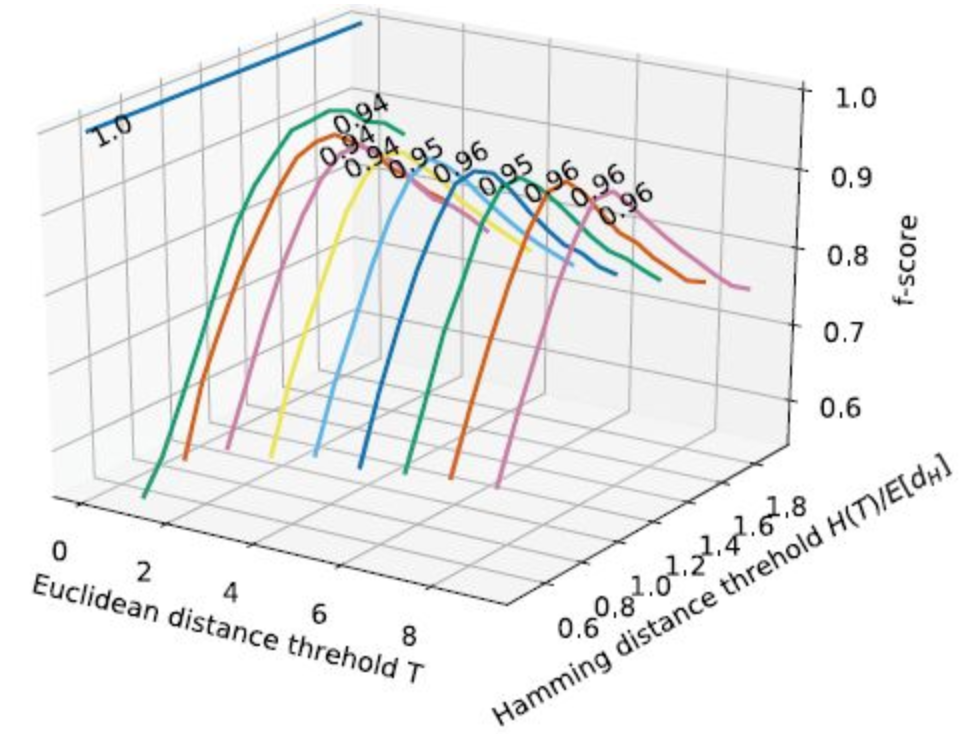
当然，这个是缺乏理论基础的，仅仅实验方式给出的数据可能因为数据集而存在偏差。

6 总结与反思

我们通常提到差分隐私的时候都是采用的 ε-DP，而在DPRL中的证明过程中却采用的 (ε, δ)-DP，为什么不用ε-DP呢？

首先，用ε-DP是可以的，不过这样的结果不太好看，在采用ε-DP的前提下，组合性质说其隐私保护程度为 [(1+p)(1-p)]^s，而 s 是一个很大的数，简单来说，就是这个结果不能看。

那么，仅仅使用ε-DP是否合理呢？我们重新看一下组合性质，文章《The algorithmic foundations of differential privacy》：

组合性质说对同一数据进行多次查询。而本方案是对RBV的结果进行的加噪处理，在RBV的方案中，随机数是给定的，我们假定 r = [3,7]，数据分布范围为 [0,10]，也就是说如果编码的第一位为0那么编码的第二位一定也是0，即编码的结果中是有着数据相关性的（前提是随机数已经给定并且不变），所以组合机制提供的仅仅是一个隐私保护的下界。

当然，并不是说使用(ε, δ)-DP就可以解决这个问题，不过结果比较好看。毕竟可以说这个方案几乎是(0,0)-DP的。直观感觉来看，给定编码的结果，是难以确定原始数据的。

---

本篇内容到这里就结束了，欢迎关注公众号《差分隐私》，获取更多前沿技术。